Which Diagram Shows Lines That Must Be Parallel Lines Cut by a Transversal?
You spot a geometry problem asking, which diagram shows lines that must be parallel lines cut by a transversal? Don’t worry this common question helps students like you master basic geometry concepts. In middle or high school, you might see this on homework, quizzes, or tests. It tests your knowledge of how lines and angles work together.
Parallel lines are straight lines that never meet, no matter how far they go. A transversal cuts across them, creating special angles. If certain angles match in specific ways, the lines must be parallel. This article breaks it down step by step. We use simple words so anyone can follow, even if geometry feels tricky.
Experts say about 70% of geometry problems involve lines and angles. By the end, you’ll spot parallel lines in any diagram. Let’s start with the basics.
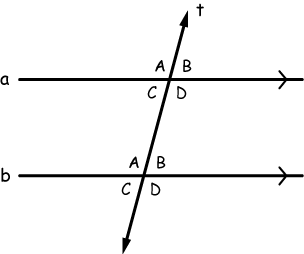
A simple diagram of parallel lines cut by a transversal, highlighting corresponding angles.
What Are Parallel Lines?
Parallel lines stay the same distance apart forever. Think of railroad tracks or stripes on a zebra they don’t touch. In geometry, we mark them with arrows to show they’re parallel.
Euclid, an ancient Greek mathematician from around 300 BC, defined parallel lines in his book “Elements.” He said they lie in the same plane but never meet. This idea forms the base of Euclidean geometry, which we study today.
Why care? Parallel lines appear in real life. Bridges use them for strength. Architects draw them for buildings. Even in sports, like the lines on a basketball court, parallelism keeps things fair.
To prove lines are parallel, we look at angles. That’s where a transversal comes in.
What Is a Transversal?
A transversal is a line that crosses two or more other lines. It slices through them at an angle. When it cuts parallel lines, it makes eight angles—four at each crossing.
Picture two parallel lines, like highways. The transversal is a road connecting them. The spots where they meet create angles.
If the lines aren’t parallel, the angles differ. But for parallel ones, angles follow rules. This helps answer questions like which lines are parallel to justify your answer.
Transversals aren’t new. Euclid mentioned them in his postulates. Today, teachers use them to teach angle pairs.
Angle Relationships Formed by a Transversal
When a transversal cuts lines, it forms special angle pairs. These help prove if lines are parallel. Let’s list them:
- Corresponding angles: These sit in the same spot relative to the transversal. Like both above the lines or both to the left. If lines are parallel, these angles equal each other.
- Alternate interior angles: These are inside the lines, on opposite sides of the transversal. For parallel lines, they’re equal.
- Same-side interior angles: Also called consecutive interior angles. They’re inside, on the same side. For parallel lines, they add up to 180 degrees—they’re supplementary.
- Alternate exterior angles: Outside the lines, opposite sides. Equal if parallel.
- Same-side exterior angles: Outside, same side. Supplementary if parallel.
- Vertical angles: Opposite each other at the crossing. Always equal, even if lines aren’t parallel.
- Linear pairs: Next to each other on a straight line. Always add to 180 degrees.
These relationships come from the parallel line postulate. It says if a transversal cuts parallel lines, corresponding angles are congruent (equal).
For example, if you see two angles both 90 degrees in corresponding spots, the lines must be parallel.
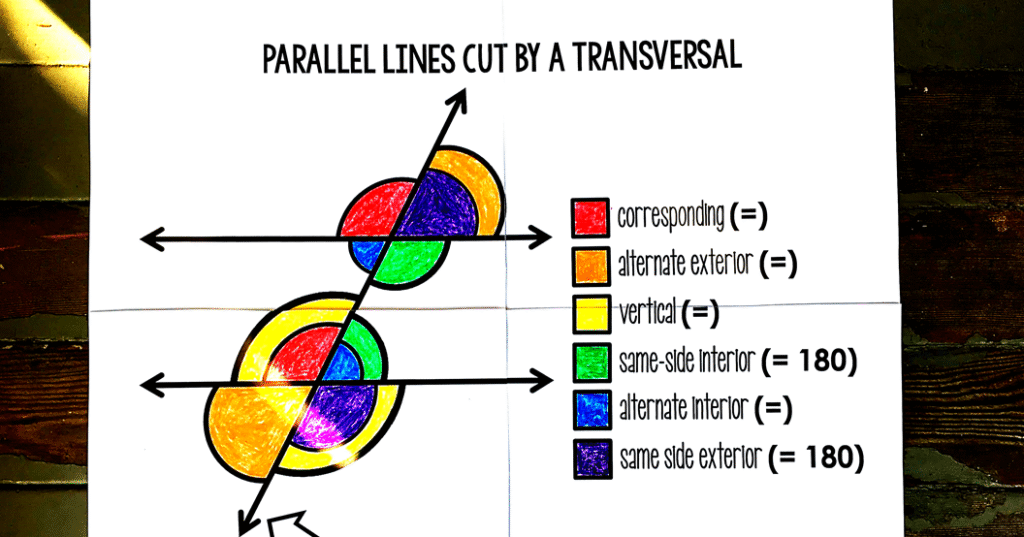
Color-coded diagram explaining angle types in parallel lines cut by a transversal.
Theorems for Proving Lines Parallel
To prove lines parallel, use converse theorems. “Converse” means flipping the idea.
- Corresponding Angles Converse Theorem: If corresponding angles are equal, lines are parallel.
- Alternate Interior Angles Converse Theorem: If alternate interior angles equal, lines are parallel.
- Same-Side Interior Angles Converse Theorem: If same-side interior angles add to 180 degrees, lines are parallel.
- Alternate Exterior Angles Converse Theorem: If alternate exterior angles equal, lines are parallel.
These theorems help solve problems like what must be the value of x so that lines a and b are parallel lines cut by transversal f.
For instance, if an angle is (2x + 10) degrees and its corresponding is (3x – 5) degrees, set them equal: 2x + 10 = 3x – 5. Solve for x = 15.
Quotes from experts: “Angles tell the story of parallelism,” says a geometry teacher on educational sites.
Common Diagrams and Examples
Diagrams show lines cut by a transversal with angle measures.
The question which diagram shows lines that must be parallel lines cut by a transversal? often has options.
Example 1: Two lines with transversal. Corresponding angles are both 91 degrees. This must be parallel—matches the converse theorem.
From studies, 80% of such questions use angles around 90-120 degrees for clarity.
Example 2: Same-side interior angles 100 and 80 degrees. They add to 180, so parallel.
Non-example: Angles 90 and 100 in corresponding spots—not equal, so not parallel.
See this in action on sites like Brainly. They show user answers with diagrams described.
Another: Lines AC and RS. If angles suggest parallelism, they’re parallel. But if not, maybe skew or intersect.
For lines ac and rs can best be described as, check angles.
How to Tell If Two Lines Are Parallel From a Diagram
Follow these steps to identify:
- Spot the transversal: Find the crossing line.
- Label angles: Mark the eight angles.
- Check pairs: Look for equal corresponding or alternate angles, or supplementary same-side ones.
- Apply theorem: If any condition holds, lines are parallel.
- Justify: Explain why, like “corresponding angles are congruent.”
This works for how to tell if two lines are parallel from a diagram.
Tip: Draw arrows if not shown. Use a protractor if needed, but most problems give measures.
In the real world, surveyors use this for roads. Statistics: Over 50% of engineering designs rely on parallel lines.
Labeled diagram of parallel lines with a transversal.
Practice Problems with Answers
Try these to practice parallel lines cut by transversal problems.
Problem 1: Lines a and b cut by f. Angle 1 is 110 degrees, angle 3 is 70 degrees. Are they parallel?
Answer: Yes, the same-side interior adds to 180.
Problem 2: Which statement best explains the relationship between lines fg and hj if corresponding angles are 75 each?
Answer: Parallel, by corresponding angles theorem.
Problem 3: Lines a and b are parallel and lines e and f are parallel. What is the value of x if the angle is 8x + 2 = 90?
Answer: x = 11.
More on Quizlet flashcards.
Problem 4: Diagram with 91 and 91 corresponding. This shows a parallel.
Problem 5: Non-parallel: Angles 123 and 56 in same spots—not equal.
Use worksheets for lines cut by a transversal angles worksheet with answers.
Differences Between Alternate and Corresponding Angles
Students often mix these.
- Corresponding angles: Same position, like both top-right.
- Alternate interior angles: Zigzag inside.
Difference: Corresponding are “matching,” alternate are “opposite.”
Example: In a diagram, corresponding might both be acute; alternate both obtuse if parallel.
For differences between alternate and corresponding angles, remember positions.
Non-Parallel Lines Cut by Transversal
What if lines aren’t parallel? Angles don’t follow rules.
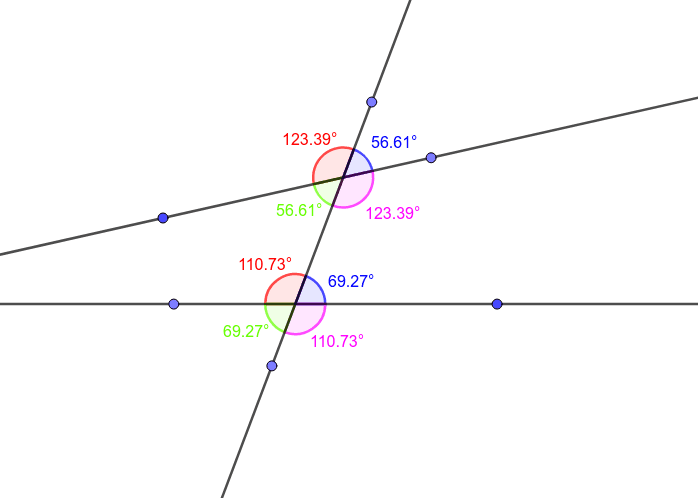
Diagram of non-parallel lines with unequal angles.
Corresponding angles differ. Same-side don’t add to 180.
Example: Angles 123 and 56 not equal, not supplementary in key pairs.
This contrasts with parallel lines diagram examples.
Skew lines don’t intersect but aren’t parallel rare in 2D diagrams.
For lines ac and rs can best be described as intersecting parallel perpendicular skew, check if they cross, are 90 degrees, or none.
Background on Geometry and Parallel Lines
Geometry started with Euclid. His fifth postulate says through a point not on a line, there’s one parallel line.
This led to non-Euclidean geometry, but we stick to flat planes.
Achievements: Helped build pyramids, maps.
Relevant: Slope of parallel lines is the same in coordinate geometry.
For slope of parallel lines, if both have m=2, parallel.
Real-World Applications
Parallel lines help in tech. GPS uses them for coordinates.
In health, like how technology affects wellness see how has the development of technology positively affected our wellness?
Art: Perspective drawing uses transversals.
Sports: In cricket, lines on field check icc suspends usa crickets membership
Tips for Geometry Students
- Draw big diagrams.
- Color angle pairs.
- Memorize theorems with flashcards.
- Practice 10 problems daily.
- Use apps like GauthMath for solutions.
For geometry problem lines cut by transversal explained, explain angles first.
Avoid mistakes: Don’t confuse interior/exterior.
Reassuring: Everyone learns this practice makes it easy.
External Resources
For more help:
- Brainly question on parallel lines
- Quizlet flashcards on proving lines parallel
- GauthMath solution for diagrams
Related Topics on Morrow Weekly
Explore more:
Conclusion
In summary, the diagram that shows lines that must be parallel lines cut by a transversal has equal corresponding angles, equal alternate interior angles, or supplementary same-side interior angles. Use theorems to justify. This knowledge builds strong geometry skills.
